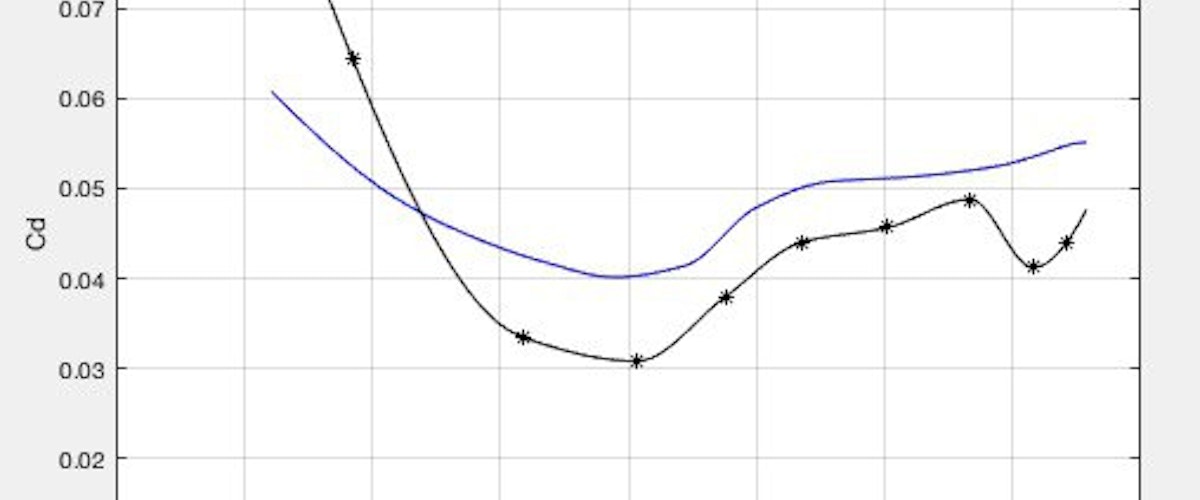
Stima della curva del coefficiente di resistenza aeredinamico

Supponendo determinate condizioni atmosferiche, le simulazioni aiutano a comprendere quale potenza di ingresso è necessaria per raggiungere una certa velocità. Dal momento che l’obiettivo è superare il record mondiale di velocità nella World Human Powered Vehicles Challenge (WHPSC) in Nevada, ottenere informazioni sulle prestazioni della bicicletta è fondamentale. Inoltre, essere in grado di simulare una corsa prima di essere effettivamente sul tracciato di gara, permette di stimare il potenziale della bici.

Queste simulazioni usano un’equazione di bilancio energetico. Data la velocità v(j) all’intervallo di tempo j-esimo, si ottiene la velocità al prossimo istante temporale risolvendo l’equazione per v(j+1). Nell’equazione si hanno i vari contributi energetici: l’energia cinetica (Ec), i contributi positivi (da potenza fornita dal ciclista e pendenza negativa) e i contributi negativi (causa resistenza al rotolamento e aerodinamica). Quest’ultimi sono rispettivamente dati da:

E_r=m*g*C_r dl
E_d=1/2*rho*A*C_d*v^2 dl

dove:

• m è la massa del veicolo
• g è la forza gravitazionale di accelerazione
• dl è la distanza coperta nell’intervallo di tempo
• rho è la densità dell’aria
• A è l’area frontale
• v è la velocità del veicolo [m/s]
• C_r è il coefficiente di resistenza al rotolamento
• C_d_ è il coefficiente dei resistenza aereodinamica

Entrambi i coefficienti dipendono dalla velocità. Se si considerano gli altri termini dell’equazione di essere “ragionevolmente corretti”, maggiore è la precisione con cui si determinano i coefficienti, maggiore sarà anche l'accuratezza con cui si simula il risultato di una corsa. I valori per la curva C_r sono ottenuti dal nostro banco prova, mentre quelli del profilo C_d sono ricavati da una una simulazione CFD.

Per questo motivo si è ritenuto importante valutare l’accuratezza della simulazione CFD (misurata sul risultato di una corsa: per semplicità, la velocità finale raggiunta*. Inoltre, siccome essa è in condizioni statiche (il veicolo è fermo, il vento arriva a differenti velocità), non si tiene conto dell'interazione tra il veicolo ed il ciclista.

È stata identificata una procedura di quattro passi in modo tale da poter determinare un profilo “realistico” basato sui dati di una corsa WHPSC, utilizzando una variabile aleatoria z adimensionale definita come

z(j)=error(j)/Ec(j+1)

dove:
errore(j) è l’errore nella j-esima equazione di bilancio energetico;
Ec(j+1) : è l’energia cinetica alla fine dell’intervallo temporale

Dapprima, al vettore z è stato applicato un filtro passa-basso e considerato un errore medio nell’equazione di bilancio energetico. Poi, si è determinato C_d risolvendo l’equazione per il coefficiente, eseguendo successivamente una media mobile sul vettore. Infine, si è campionato il vettore C_d (che contiene valori a velocità differenti), mantenendo un numero ragionevole (circa 10), uno ogni circa 15-20 km/h.

Di seguito sono riportati i grafici ottenuti. Differiscono leggermente per alte velocità (circa 35 m/s), rimanendo abbastanza simili per il resto. Notare che la scala degli assi è stata alterata.

*nella competizione viene determinata la velocità media sugli ultimi 200 metri

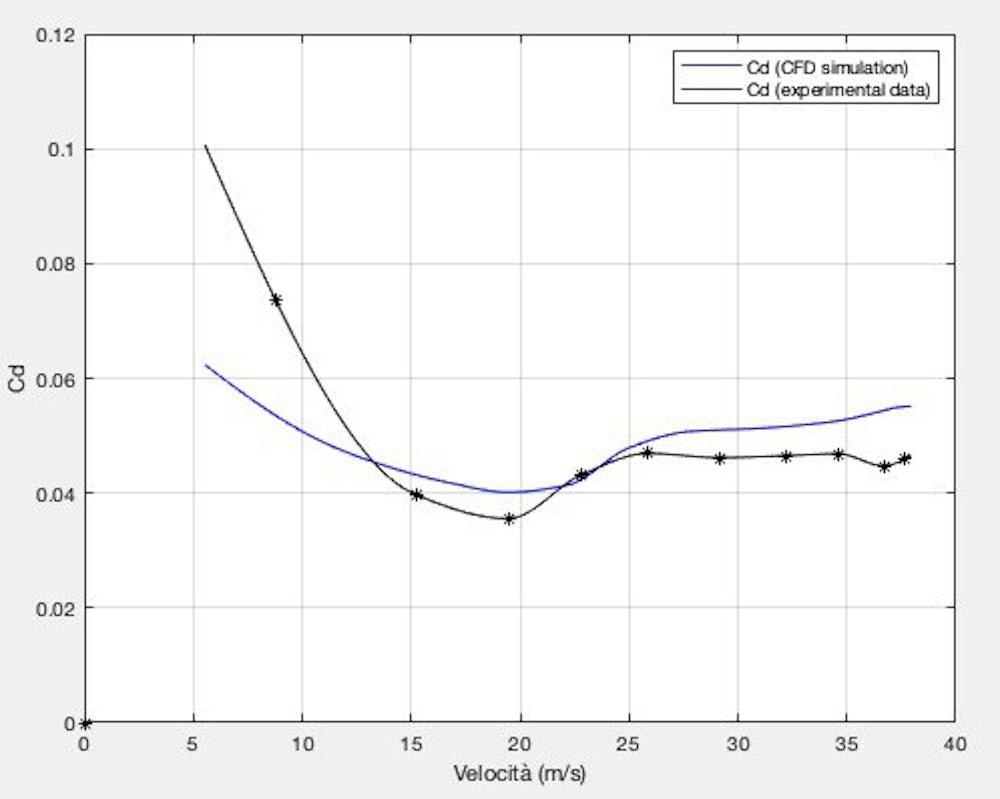
Drag coefficient (BM 19 Thursday PM ride)

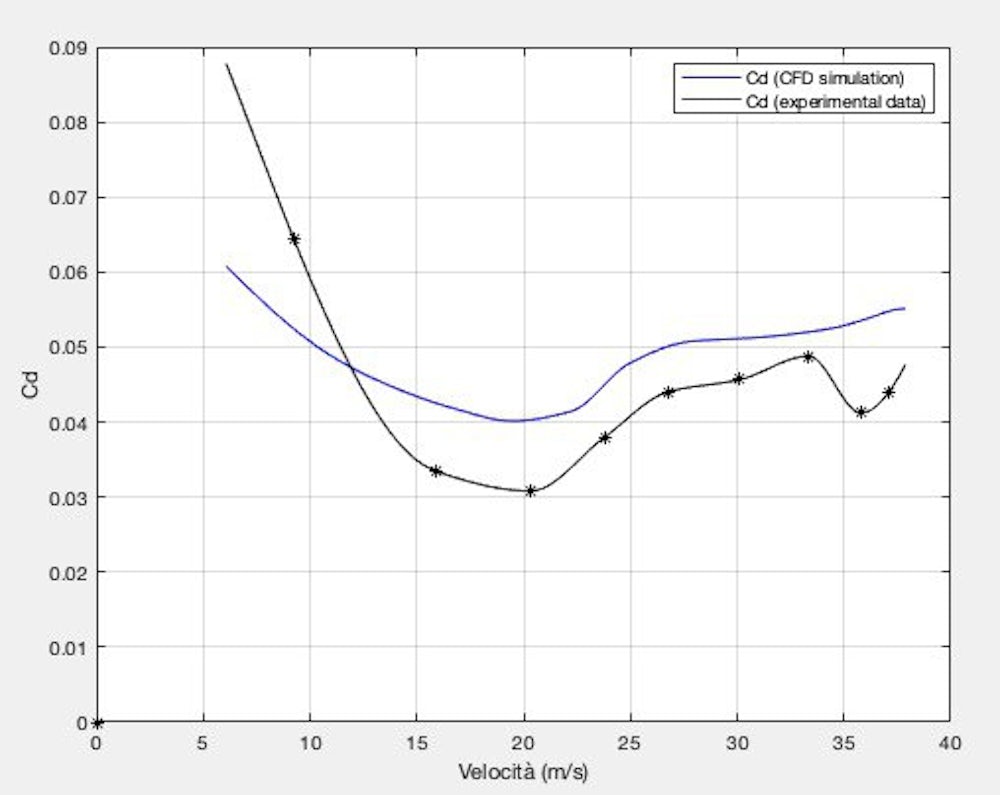
Drag coefficient (BM 19 Friday PM ride)